高效深度神经网络测试的实用准确度估计
摘要
深度神经网络 (Deep neural network, DNN) 愈发流行,DNN的测试对DNN的正确性(即DNN在指定工作中的准确度)至关重要。然而,DNN 测试存在严重的效率问题,即,标注每个测试输入以了解DNN在测试集上的准确度的成本很高,因为需要大量的人(甚至他们还需要特定领域知识)来对测试数据进行手工标注,而测试集本身又是大规模的。为缓解此问题,本文提出了一种叫PACE新颖手法(Practical ACcuracy Estimation的缩写),其选择一小部分测试输入,可以精确地估计整个测试集的准确性。这样一来,只需对这小部分选定样本进行标注即可,这很大程度上降低了标注成本。除了实现精确的准确性估计外,为使PACE更加实用,其还被要求应该是可解释的、确定的,并尽可能地高效的。因此,PACE首先结合聚类,将具有不同测试能力(即测试DNN模型不同功能)的测试输入划分为不同的组。然后,PACE利用MMD-critic算法(一种最先进的基于样例的解释算法,根据组的大小,从每组中选择原型,即选择最具代表性的测试输入)来可以减少聚类带来的噪音影响。同时,PACE还使用了自适应随机测试的思想,从少数空间(即没有聚成任何一组的测试输入)中选择测试输入,以保证在所需的测试输入数量下实现极大的多样性。两个平行的选择过程(即同时从组和少数空间中进行选择)组建了最终的一小部分被选中的测试输入集合。结果表明,PACE能够精确估计整个测试集的准确性,平均偏差只有1.181%∼2.302%,大大超过了最先进的方法。
简介
本文共做出以下主要贡献:
方法。我们提出了第一个相对可解释、确定和有效的叫做PACE的方法,通过选择DNN测试输入的子集来估计整个测试集的准确性。
实现。我们基于最先进的框架和库实现了所提出的方法,包括Keras 2.2.4和TensorFlow 1.14.0,以及hdbscan 0.8.22、sklearn与MMD-critic算法的作者分别提供的HDBSCAN、FastICA和MMD-critic算法。
研究。我们基于测试和测试集下的24对DNN模型进行了广泛的研究,这些测试考虑了模型和测试输入的多样性,证明了PACE的有效性。
制品。我们已经发布了一个广泛的数据集,供未来使用和研究,其中包括了我们的实现以及实验数据。
方法
为了提高 DNN 测试的效率,我们的目标是选择测试输入的子集来代表整个测试集,即我们希望通过只标记一小部分选定的测试输入来精确估计整个集合的准确性。这可以大大降低标注成本。然而,如何有效地选择这样一小组测试输入是具有挑战性的。此外,选择的方法要尽可能具有可解释性、高效性和确定性,以使其适用于实践。这也是解决这个问题的关键挑战。
在本文中,我们提出了一种新颖实用的方法,称为 PACE,用于从测试输入集中选择更小的子集。一般来说,对于整个测试集,一些测试输入具有相似的测试能力(即测试 DNN 的相似功能),而一些测试输入具有不同的测试能力。直观地说,所选的一小部分测试输入应该涵盖各种测试能力,并保证它们对应的测试能力的原始分布,以使得这些样本能尽可能地代表整个集合,并具有高可解释性。为了实现这个目标,PACE根据识别的特征将所有的测试输入聚类成组,从中反映它们的测试能力,其中不同的组更有可能具有不同的测试能力。由于组的大小在一定程度上反映了不同测试能力的分布,PACE根据不同组大小的比例选择所需的测试输入数量,以保持测试能力的相似分布。
一个自然的后续问题是应该从每组中选择哪些测试输入。由于很难通过聚类来完美区分具有不同测试能力的测试输入,我们应该选择最能反映该组测试能力的测试输入,来绕过每组中噪音的影响。为了进一步增强所选测试输入的可解释性,PACE利用最先进的基于样本的解释算法MMD-critic算法来从每组中选择原型(即最具代表性的测试输入)。此外,也可能有一些测试输入不属于任何一组。也就是说,它们中的每一个都可能有独特的测试能力。我们称这些测试输入的空间为少数空间。从少数空间中选择测试输入是合理的,因为它们能更进一步接近整个测试集。为了使用所需数量的测试输入更充分地探索少数空间,PACE 借用了自适应随机测试的思想来选择测试输入。
图1展示了我们的方法PACE的概况。
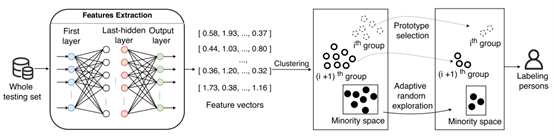
图1 PACE概况
特征研究
我们首先确定测试输入的特征,来区分它们的测试能力。根据传统软件测试,有两类特征可以在一定程度上反映测试能力,即覆盖率特征和输入特征。对于DNN测试,前者指的是在执行测试输入时,哪些DNN元素被覆盖,而后者不依赖于覆盖信息,而是依赖于测试输入信息。本工作中,我们使用输入特征来帮助区分测试能力。主要原因有以下三个:(1)现有的工作已经证明,对于一个给定的DNN来说,许多测试输入可能具有非常相似的神经元覆盖率,因此覆盖率特征不能很好地判别其测试能力。(2)在选择测试输入的问题上,已有工作对覆盖率特征的有效性进行了评估,结果表明其有效性比输入特征的有效性要差。(3)收集覆盖率特征往往会产生额外的代价。
DNN逐渐从输入中学习特征来预测标签。DNN的不同层代表不同类型的输入特征。越接近输入层的层代表更多的基本特征,而更接近输出层的层则代表更多的高阶特征。也就是说,测试输入信息包含基本信息(即测试输入本身和从测试输入提取的基本特征)以及高级信息(从测试输入中提取的高阶特征)。更多的高阶特征可以更精确地捕捉到输入和标签之间的关系,但它们更特定于给定的DNN模型,且由于他们需要运行更多层的DNN模型,收集它们的成本更高。相比之下,更基本的特征更通用,其也可更有效地收集,但它们不能反映更复杂的输入特征模式来预测标签。我们的方法并不特定于指定类型的输入特征,本工作中也研究了不同类型的输入特征。本文主要研究以下四种不同类型的输入特征(包括基本特征和高阶特征)为代表:
原始特征(ORI):指的是一个DNN的输入向量,其是最基本的特征,直接代表一个输入本身。
第一层特征(FL):指的是DNN中第一层的输出,最接近DNN的输入向量。
最后隐藏层特征(LHL):指的是DNN中最后一个隐藏层的输出,是可以直接推断输入对应的预测结果的高阶特征。
置信特征(CON):指的是DNN(分类器)的输出,其表示预测结果的置信度。我们还将其归入输入特征中,因为其不依赖覆盖率信息,而是依赖通过DNN模型从测试输入中得到的输出。
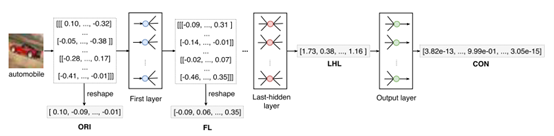
图2 特征提取可视化
图2使用一个输入样例(CIFAR-10中的汽车图像)说明了DNN中每种类型的特征来源。请注意,DNN的输入和DNN中某些层的输出可能是多维矩阵,因此我们将矩阵降维成向量作为特征向量(如图2中的ORI和FL)。特别的,ORI特征是静态特征,它们不需要运行DNN,而FL、LHL和CON特征都是动态特征。
基于聚类的测试能力鉴别
基于识别出的测试输入特征(如ORI或FL),每个测试数据皆以一个特征向量来表示。PACE将测试输入聚类到不同组中,以根据特征向量集区分它们的测试能力。聚类前,我们首先对特征进行归一化,以将不同尺度上测量的值调整至同一尺度上。由于特征都是数字类型,PACE采用min-max归一化方法,将这些特征的每个值调整到区间[0,1]中。假设整个测试集表示为T,其大小为st,T中的测试输入集表示为T={t1,t2,…,tst},ti的特征向量表示为Fi={fi1,fi2,…,fir},我们用变量xij表示归一化前ti的第j个特征值,用变量x*ij表示归一化后ti的第j个特征值(1≤i≤st且1≤j≤r)。下式展示了归一化的计算过程:
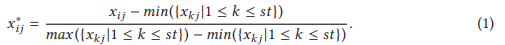
PACE之后采用HDBSCAN(基于分层密度的噪声应用空间聚类)算法来对测试输入进行聚类,原因如下。(1)几乎不可能事先知道测试能力类型的数量,因此需预先定义集群数量的聚类算法无法使用,如广泛使用的K-means算法。HDBSCAN不需要预先定义聚类的数量,而是基于密度进行聚类。(2)最广泛应用的基于密度的聚类算法之一是DBSCAN,而HDBSCAN是其升级版。特别的,HDBCSAN可以有不同密度的簇,而DBSCAN必须预先定义簇的密度。(3)HDBSCAN已被证明是十分高效的,使我们的方法PACE更加实用。(4)HDBSCAN需要设置的参数很少,并且对参数选择具有鲁棒性。这使得它在实践中更容易使用。
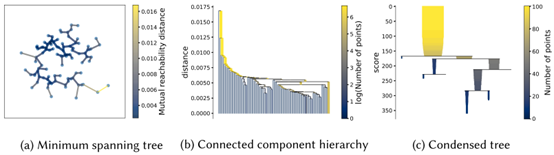
图3 HDBSCAN聚类主要阶段的可视化
HDBSCAN是一种基于密度的聚类算法,它将紧密堆积在一起的数据点(即有许多附近邻居的数据点)分组。为了更清楚地说明PACE在HDBSCAN的过程,我们将DNN模型ResNet-20的测试集CIFAR-10中抽取100个测试输入,对HDBSCAN聚类的主要阶段进行可视化(如图3所示)。更具体地说,其首先构建一个加权图,其中数据点是顶点,任意两点间都存在一条边,其权重等于两点之间的相互可达距离。下式显示了基于K近邻的点a与点b之间的相互可达距离(MRD)的计算:
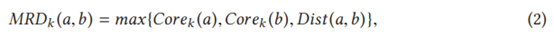
其中Corek(a)和Corek(b)分别代表a/b与其第k个最近邻之间的距离;Dist(a,b)是a和b之间的距离,用广泛使用的欧几里得距离测量。在MRD下,密集点之间的距离保持不变,但稀疏点被移动至与其他点的距离至少为他们的core距离。然后,HDBSCAN通过Prim算法构建加权图的最小生成树,如图3(a)所示。在最小生成树的基础上,通过对树边按距离升序排列,并通过为每条边创建一个新的合并簇进行迭代,将一个完全联通的图转化为一个连通分量的层次结构,如图3(b)所示。接下来,其根据最小集群大小(HDBCSAN的一个参数)将大集群层次结构压缩为较小的树,如图3(c)所示。最后,它通过计算每个聚类的稳定性分数,从树中提取稳定的簇。基于HDBCSAN,PACE将测试输入分为不同的组,不同的组更可能具有不同的测试能力。此外,一些输入没有被聚类到任何组中,构成了少数空间。
请注意,当特征维度增加时,HDBCSAN的性能可能会大大降低。因此,PACE在聚类前结合了对高维特征进行降维的过程。更具体地说,PACE使用FastICA算法来进行降维。FastICA旨在通过最大化公式(3)中所定义的负熵来找到独立成分,并有助于找到潜在因素。在这个公式中,YGauss是一个方差与随机变量Y相同的高斯随机变量,E[.]是计算均值,而g(.)是一个非线性函数,用以近似微分熵:
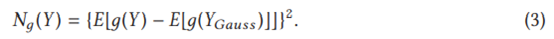
基于MMD-critic的原型选择
在将具有不同测试能力的测试输入分为不同组后,PACE再从每个组中选择测试输入,构成测试输入的小集合。由于很难通过聚类来完美区分不同的测试能力,每组都可能存在噪声,即不应将这个测试输入划分到该组的情况。为了绕过每组噪声的影响,可选择最能代表该组测试能力的测试输入,它们也被称为原型。为增强每组所选测试输入的可解释性,PACE利用MMD-critic算法,一种最先进的基于样本的解释算法(用于机器学习模型的可解释性,包括分类和聚类),来从每组中选择原型。
更具体地说,它通过计算原型分布(表示为P)和组分布(表示为G)之间的差异来选择原型。所选的原型应具有最小差异。MMD是P和G之间差异的度量,由两个分布期望间差异的函数空间F上的上限值给出,如下式所示。此外,PACE还基于MMD-critic算法选择criticism(criticism指不具代表性的样本),即与该组原型差异最大的测试输入。criticism与原型能够帮助开发人员建立更好的模型来理解组,从而可以提高选择的可解释性:
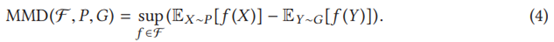
通过这种方式,PACE从每组中选择所需数量的原型来构成小集合,同时也选择相应的criticism来帮助理解簇中复杂的测试输入空间。
少数空间的自适应随机探索
少数空间的测试输入也是整个测试集的组成部分,因此,所选择的小集合也应该包含这些测试输入的一部分,以更好地代表整个测试集。而选择这些测试输入的一部分来代表整个少数空间是具有挑战性的,因为这些测试输入可能彼此具有不同的测试能力。为使用所需数量的测试输入来尽可能充分探索少数空间,PACE借用了自适应随机测试的思想。这样,PACE就可以在所需的测试输入数量下实现极大的测试能力多样性,从而使整个少数空间尽可能由所需的测试输入数量来表示。更具体地说,它计算未选择的测试输入与每个已选择的测试输入之间的距离,并使用最小距离作为未选择的测试输入与已选择测试输入的距离。然后,它选择与已选择的测试输入具有最大距离的测试输入作为下一个样本。在现有研究中,这种自适应随机策略以及被证明比其他自适应随机策略更有效。根据聚类中使用的距离,PACE还使用欧几里得距离来计算测试输入之间的距离。下式给出了每次选择时的计算结果,其中U和S分别代表未选择的测试输入集和已选择的测试输入集,EucDist(,)旨在计算两个测试输入间的欧几里得距离。
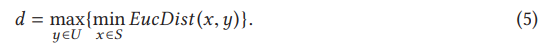
传统的自适应随机测试随机选择第一个样本,但PACE确定性地选择第一个测试输入,使其更具实用性和可解释性。更具体地说,PACE选择具有最独特测试能力的测试输入作为第一个样本,其与所有组的距离最大。特别的,该测试输入是通过基于HDBSCAN聚类算法提供的outlier_scores(测量与所有组的距离)值来对少数空间中的测试输入进行排名后,处于Top-1位置所对应的输入。
PACE的使用
本小节中,我们介绍PACE用法,算法1是PACE的高级伪代码。PACE的输入包括一个表示为D的被测试的DNN,一个表示为T的完整测试集,其大小表示为st,以及表示所选测试输入小集合大小,表示为n。为了构建可以精确估计整个测试输入的准确度的小集合,PACE首先通过提取特征(如ORI或FL)将每个测试输入转换为特征向量(如算法1的2-4行所示)。然后,PACE对向量集进行包括归一化或降维的预处理,并通过聚类将其分为m组和少数空间(算法1中的第5行和第6行)。再次,我们表示第i个组的大小为si,少数空间的大小为sm,其中:
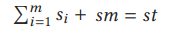
选定的小集合测试输入应包含来自每个组的测试输入和来自少数空间的测试输入。在这里,我们定义了一个阈值α来确定他们的比例分布。也就是说,从组中选择的测试输入数量是α·n,而从少数空间中选择测试输入的数量是(1-α)·n(小于sm)。此外,PACE根据不同组大小的比例从每个组中选择测试输入,以保持测试能力的相似分布。即从第k组中选择的测试输入的数量是:
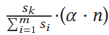
在确定每个组或少数空间中选择的测试输入数量后,PACE根据基于MMD-critic的原型选择方法(算法1中的第7-11行)或自适应随机选择方法(第12-14行)来选择构建一小组测试输入,即PACE的输出(算法1中的第15行)。开发人员只需标注这一小组测试输入即可在实践中估计整个测试集的准确性。

结论
为提高深度神经网络(DNN)的测试效率,我们的目标是选择一小组可以精确估计整个测试集准确性的测试输入。我们只需标注这个小集合,而不必标注整个测试集。为了实现这一目标,我们提出了PACE,一种新颖而实用的方法来选择小集合测试输入集。为了使PACE更加实用,PACE结合了聚类,将不同测试能力的测试输入聚为不同组,然后利用MMD-critic算法从每个组中选择原型,并借助自适应随机测试思想,通过考虑样本下从少数空间(即没有聚类到任何组的测试输入)选择测试输入,以构成最后的小测试输入集合。结果表明,PACE 实现了很好的准确度估计效果。
